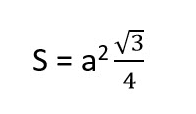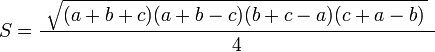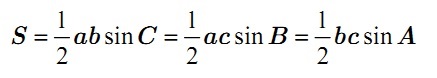Xin chào các bạn! Hôm nay trong bài viết này, mình sẽ cùng các bạn cùng nhau ôn tập lại công thức tính diện tích tam giác nhé. Như các bạn cũng đã biết và đã được học ở chương trình kiến thức. Thì tam giác có 4 loại tam giác cơ bản như: Tam giác thường, tam giác vuông, tam giác cân, tam giác đều.
Theo đó, với các loại tam giác khác nhau, chúng ta lại phải áp dụng một công thức tính diện tích khách nhau. Vì thế trong bài viết này, mình sẽ cùng các bạn ôn lại các công thức và cách tính diện tích tam giác một cách đầy đủ và chi tiết nhất. Giúp các bạn nhớ lại các kiến thức đã học và áp dụng vào thức tế cùng như vào các bài toán tính diện tích tam giác nhé.
1. Công thức tính tam giác thường
Diện tích tam giác bằng 1 phần 2 tích của chiều cao hạ từ định với độ dài cạnh đối diện của đỉnh đó:
S(ABC) = 1/2*a*h
Trong đó:
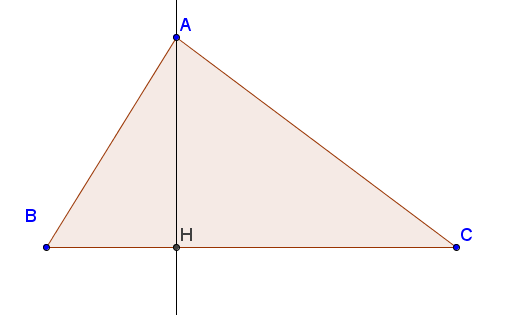
- a: Là chiều dài cạnh đáy của tam giác. (ví dụ là cạnh BC trong hình dưới)
- h: Là chiều cao từ đỉnh xuống cạnh đáy của tam giác. (ví dụ là cạnh AH hình dưới)
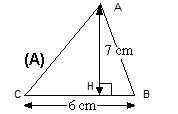
Bài tập ví dụ: Hãy tính diện tích hình tam giác ABC (hình số 1) trên biết: AH=7cm. BC=6cm.
Bài giải: Áp dụng công thức tính diện tích hình tam giác thường ta sẽ có diện tích hình tam giác ABC như sau:
S(ABC) = 1/2*BC*AH =1/2*6*7 =21 cm^2
Trường hợp 2: Ngoài ra, chúng ta có một trường hợp nữa đó là chiều cao tam giác ở ngoài hình tam giác. Như trường hợp ở trên thì là chiều cao nằm trong hình tam giác. Vậy với chiều cao nằm ngoài tam giác chúng ta sẽ có công thức như sau:
Như hình trên ta sẽ có công thức tính diện tích hình tam giác có chiều cao nằm ngoài như sau:
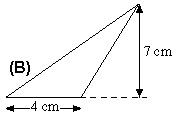
S(B) = 1/2 * 4 * 7 = 14 cm^2
Xem thêm: Công thức tính diện tích hình thoi và chu vi hình thoi
2. Tính diện tích tam giác vuông
Đối với tam giác vuông, chúng ta sẽ có công thức tính diện tích hình tam giác vuông như sau:
S(ABC) = 1/2* AB * BC
Chúng ta cũng có thể áp dụng luôn công thức tính diện tích tam giác thường như trên.
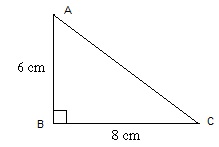
Ví dụ: Chi hình tam giác vuông ABC như hình trên. Biết AB=6cm và BC=8cm tính diện tích hình tam giác ABC.
Bài giải: Áp dụng công thức tính diện tích hình tam giác ta có:
S(ABC) = 1/2* AB * BC = 1/2 * 6 * 8 =24 cm^2
3. Diện tích tam giác đều
Với tam giác đều là tam giác có chiều dài 3 cạnh bằng nhau. Do đó, chúng ta có thể áp dụng dễ dàng định lý Heron và suy ra công thức như sau:
Trong đó với a là chiều dành của cạnh tam giác.
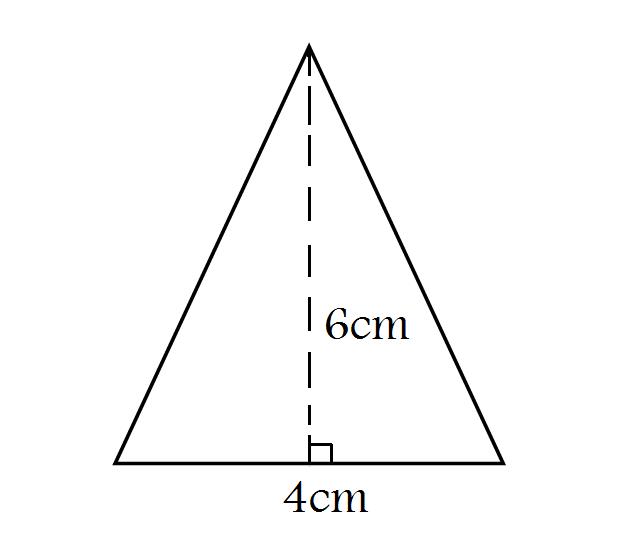
4. Diện tích tam giác cân
Với tam giác cân, chúng ta có công thức tính diện tích tam giác cân như sau:
S(ABC)= 1/2*a*h
Trong đó:
- a: Là độ dài cạnh đáy tương ứng với đường cao kẻ từ đỉnh đối diện.
- h: Là độ dài đường cao tương ứng.
Xem thêm: Công thức tính thể tích hình trụ – diện tích xung quanh và toàn phần hình trụ tròn
5. Một số cách tính diện tích khác
Diện tích tam giác khi biết 3 cạnh a b c
Với đề bài cho biết chiều dài 3 cạnh của tam giác. Thì khi đó cách tính diện tích của tam giác chúng ta sẽ áp dụng công thức Heron đã được chứng minh như sau:
Với p = (a +b +c)/2
Hay chúng ta cũng có thể biết lại bằng công thức:
Trong đó: a, b, c lần lượt là độ dài của 3 cạnh tam giác.
Tính diện tích tam giác theo sin
Với cách tính diện tích hình tam giác theo sin thì diện tích hình tam giác sẽ bằng 1 phần 2 tích của 2 cạnh kề nhân với sin của góc được tạo bởi 2 cạnh đó. Ta có công thức tính như sau:
Như vậy là trên đây chúng ta đã tìm hiểu và ôn lại kiến thức về công thức và cách tính diện tích hình tam giác: thường, vuông, cân đều một cách chi tiết và tổng quan rồi. Hi vọng với các công thức này sẽ giúp các bạn ôn tập lại kiến thức đã học và áp dụng một cách tốt nhất. Chúc các bạn thành công!
